Use of the Fock expansion for ¹state wave functions of two-electron atoms and ions

Authors

• James M. Feagin, University of Nebraska-LincolnFollow
• Joseph Macek, University of Nebraska - Lincoln
• Anthony F. Starace, University of Nebraska-LincolnFollow

Document Type

Article

Date of this Version

12-1-1985

Comments

Published by American Physical Society. Phys. Rev. A 32, 3219 (1985). http://pra.aps.org. Copyright © 1985 American Physical Society. Permission to use.

Abstract

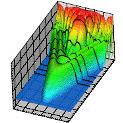
The exact representation of a two-electron wave function near the origin is the Fock expansion, i.e., a double summation over powers of R and of lnR [where R≡(r₁²+r₂²)^1/2] with coefficients dependent on the five remaining angular variables. Using a representation of hyperspherical harmonics, we present here the first numerical solution of the equations for the Fock coefficients. We present also a general procedure for matching a linear combination of Fock-series solutions onto a basis of adiabatic hyperspherical functions at a matching radius R₀. This matching procedure ensures that the proper asymptotic boundary conditions are satisfied. Exploratory numerical results are presented for ¹S wave functions of He and H^- in which four Fock-series solutions are matched onto the lowest ¹S adiabatic hyperspherical wave function at a matching radius near the first antinode in the adiabatic wave function.